大家好，我是大头，职高毕业，现在大厂资深开发，前上市公司架构师，管理过10人团队！
我将持续分享成体系的知识以及我自身的转码经验、面试经验、架构技术分享、AI技术分享等！
愿景是带领更多人完成破局、打破信息差！我自身知道走到现在是如何艰难，因此让以后的人少走弯路！
无论你是统本CS专业出身、专科出身、还是我和一样职高毕业等。都可以跟着我学习，一起成长！一起涨工资挣钱！
关注我一起挣大钱！文末有惊喜哦！

关注我发送“MySQL知识图谱”领取完整的MySQL学习路线。
发送“电子书”即可领取价值上千的电子书资源。
发送“大厂内推”即可获取京东、美团等大厂内推信息，祝你获得高薪职位。
发送“AI”即可领取AI学习资料。

MySQL零基础教程

本教程为零基础教程，零基础小白也可以直接学习。
基础篇和应用篇已经更新完成。
接下来是原理篇，原理篇的内容大致如下图所示。

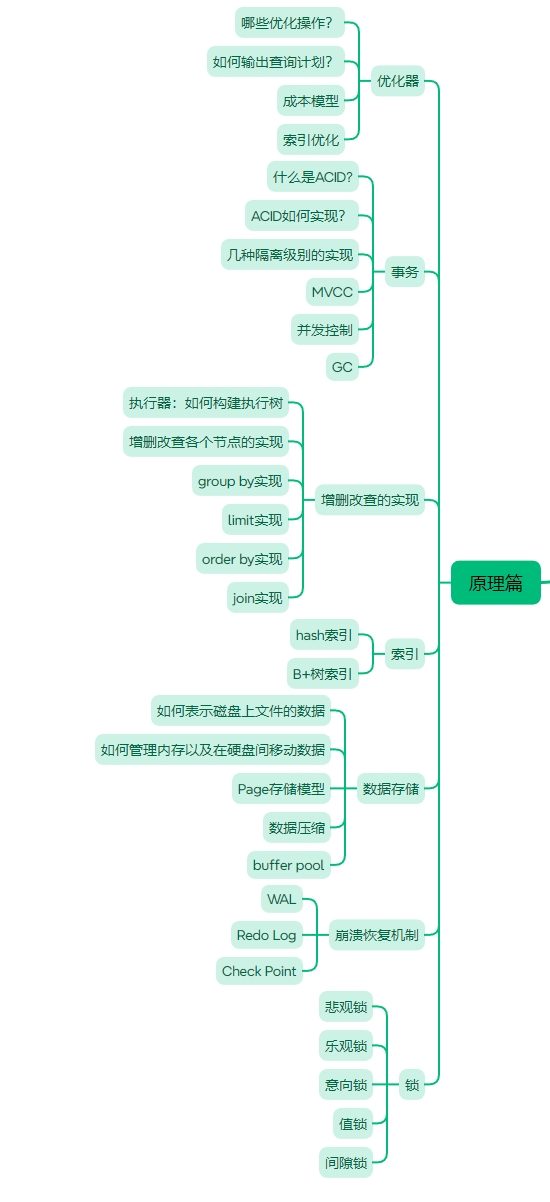
零基础MySQL教程原理篇之B+树索引

在MySQL数据库中，索引是提升查询效率的核心工具。没有索引的查询，就像是在浩瀚的书海中翻书，效率低下。而良好的索引设计，则能帮助我们高效地找到我们需要的信息，避免无谓的资源浪费。因此，理解索引的原理、种类以及如何设计索引是每个开发者必须掌握的基础技能。

索引是什么？

索引是一种数据结构，它通过特定的方式排列数据，以便于快速查询。可以把索引想象成一本书的目录，通过目录可以快速找到你想要的章节，而不用从头到尾翻书。

在MySQL中，索引通常是通过B树或B+树等数据结构实现的，数据库查询引擎可以利用这些结构快速查找数据。

B+树索引（B+ Tree Index）

这里先搞清楚一些概念，什么是b树,b+树，b*树还有b link树。

b tree(1971)：B-Tree (Balanced Tree) 是一种自平衡的多路搜索树，由 Rudolf Bayer 和 Edward M. McCreight 在 1971 年提出。
b+ tree (1973):B-Tree(Balanced Tree) 的变种，由 Rudolf Bayer 在 1973 年提出，主要改进了数据存储方式，因此大多数的数据库都使用这个作为索引。
b* tree (1977): 对 B+Tree 的进一步优化，主要的优化思路是提高空间利用率，同样的数据，可以使用更小的空间存储。
b link tree (1981): 由 Lehman 和 Yao 在 1981 年提出，在b+树的基础上，主要解决了并发控制问题。数据库中的b+树也做了一些优化，参考了b link tree的一些优点。

b tree

首先来看一下b树，这个是B+树的鼻祖了。

多路结构：每个节点可以有多个子节点（不像二叉树最多2个）
平衡性：所有叶子节点都在同一层
动态调整：插入删除时自动保持平衡

规则：

每个节点最多有 m 个子节点（m 阶）
除根节点外，每个节点至少有 ⌈m/2⌉ 个子节点
所有叶子节点在同一层
节点中的键值有序排列

优点：

减少 I/O 操作（宽而浅的结构）
适合磁盘存储
查询、插入、删除都是 O(log n)

示例图如下：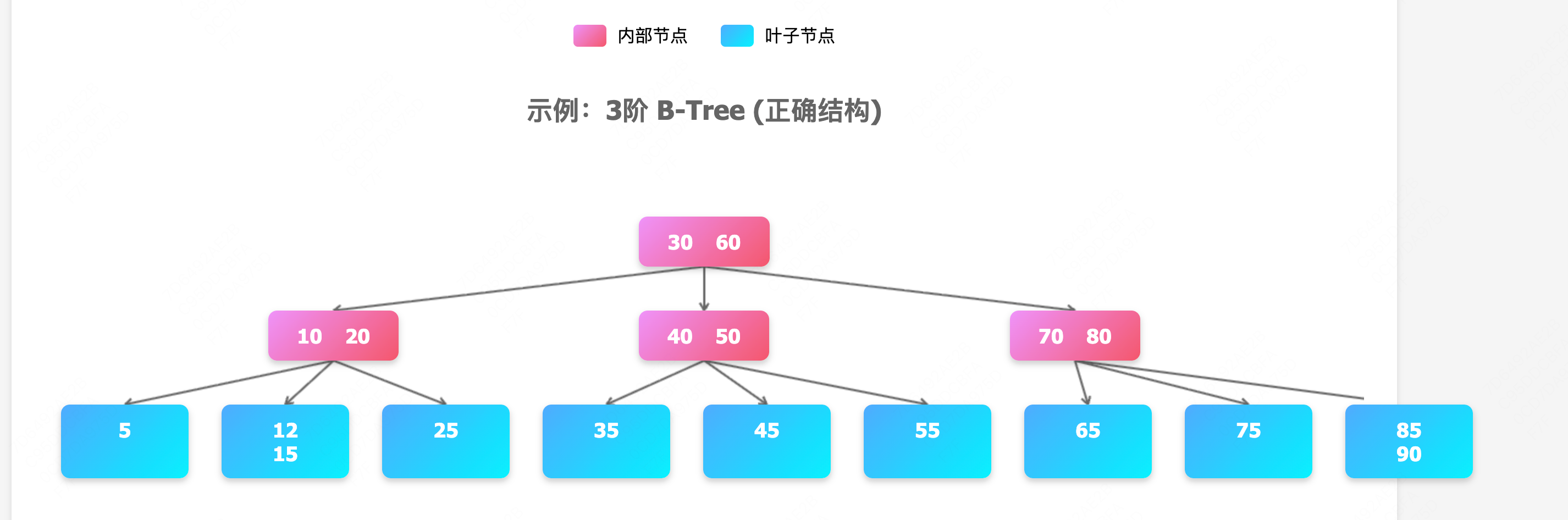

b* tree

B*树是一种m阶的平衡多路搜索树
除根节点外，所有节点的关键字个数至少为⌈(2m-1)/3⌉
所有叶子节点都在同一层
非叶子节点只存储索引信息，不存储实际数据
所有数据都存储在叶子节点中

特性	B树	B+树	B*树
数据存储	内部节点和叶子节点都存数据	只有叶子节点存数据	只有叶子节点存数据
节点利用率	至少50%	至少50%	至少66.7%
叶子节点连接	无	有链表连接	有链表连接
空间效率	一般	较好	最好
范围查询	需要中序遍历	效率高	效率高

关键特性

高节点利用率

每个节点至少2/3满（除根节点外）
相比B+树的1/2要求，空间利用率提高33%

延迟分裂策略

节点满时优先向兄弟节点转移关键字
只有兄弟节点也满时才进行分裂操作
减少了分裂操作的频率

更好的缓存性能

更高的节点利用率意味着更少的节点数量
减少了磁盘I/O操作
提高了缓存命中率

主要优势

空间效率：相同数据量下，B*树的高度更低
查询性能：更少的磁盘访问次数
插入性能：延迟分裂减少了树结构的调整
存储成本：更高的空间利用率降低存储需求

示例图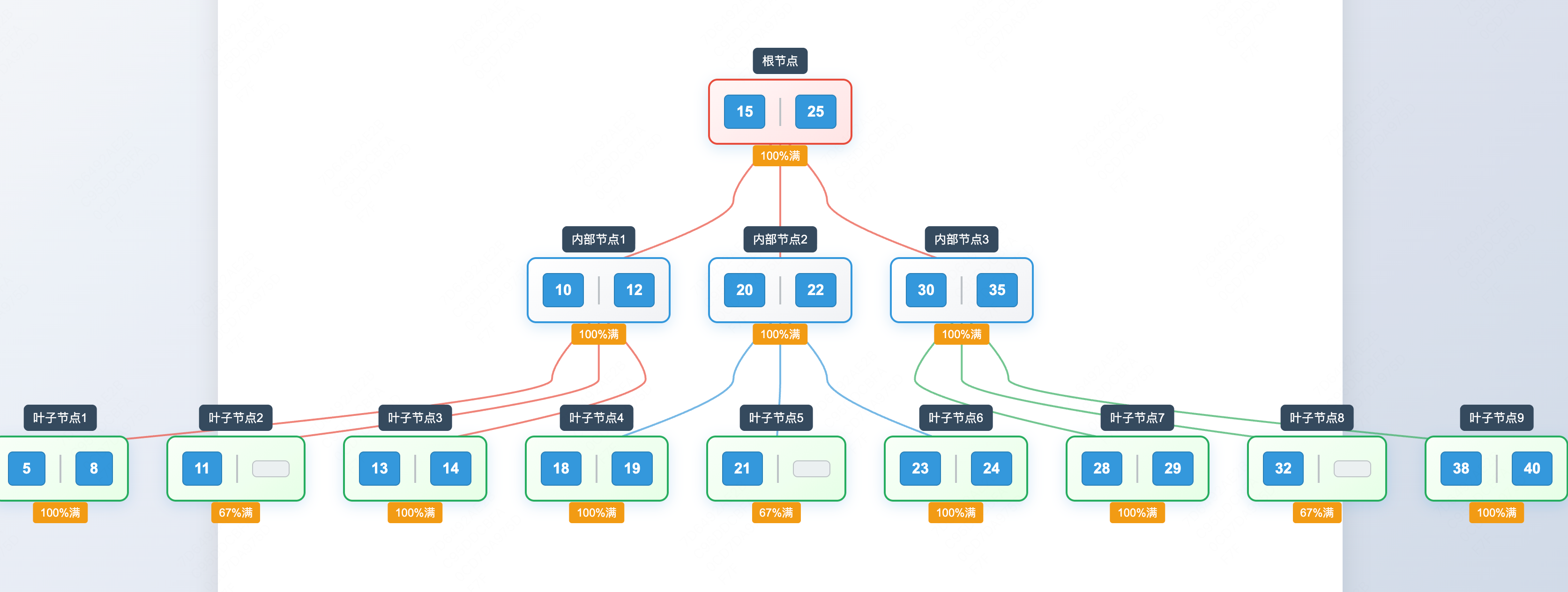

b link tree

B-link树（B-link tree）是B+树的一种变形，由Lehman和Yao在1981年提出。它是专门为支持高并发访问而设计的B+树变种。

基本定义：

B-link树是一种支持并发操作的平衡多路搜索树
在传统B+树的基础上增加了链接指针（link pointer）
每个内部节点都有一个右链接指针，指向其右兄弟节点
支持无锁或低锁的并发读写操作

并发安全的设计理念
B-link树的核心设计思想是通过右链接指针和高水位标记来实现并发安全：

Right-Link指针

每个节点都有指向右兄弟的指针
形成同一层级的有序链表
允许在节点分裂过程中继续安全访问

High Key（高水位键）

每个节点维护一个最大键值
用于判断搜索是否需要跳转到右兄弟
解决并发分裂时的一致性问题

关键设计原则

设计原则：

结构不变性：树的基本结构在并发操作中保持稳定
单向链接：只需要右链接，简化了维护复杂度
原子操作：关键操作通过原子性保证一致性
乐观并发：减少锁的使用，提高并发性能

并发控制策略

读操作：几乎无锁，可以并发执行
写操作：最小化锁的范围和时间
分裂操作：通过两阶段提交保证一致性

特性	传统B+树	B-link树
节点结构	[K1	P1
并发控制	需要复杂的锁机制	最小化锁使用
读操作	可能需要读锁	几乎无锁
写操作	需要写锁，可能阻塞读	短时间锁，不阻塞读
分裂操作	需要锁定多个节点	原子操作，影响最小
空间开销	较小	每个节点额外一个指针
实现复杂度	相对简单	较复杂

示例图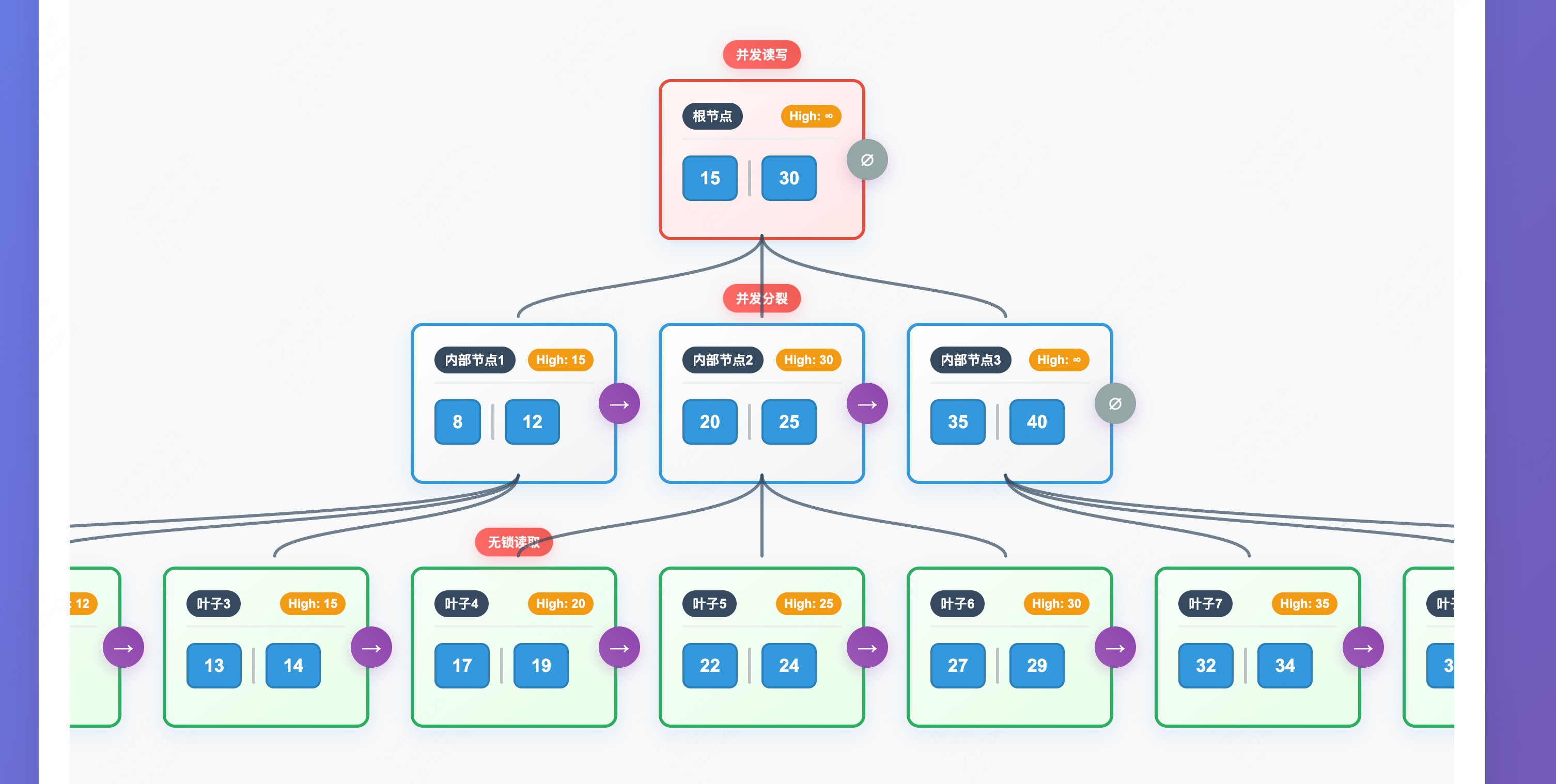

关于b link tree可以阅读论文：https://dl.acm.org/doi/pdf/10.1145/319628.319663

b+树

关于b+树的b，到底是什么意思，其实作者并没有一个明确的定义，有的人觉得是balance (平衡)，有的人觉得是Bushy（茂密）。

不过大多数人都更认同balance这个解释。

推荐一个paper：the ubiquitous B-tree

MySQL中的B+树其实和传统的还是有一点区别，比如它借鉴了b-link tree的兄弟节点的概念。

b+ tree 删除和插入的复杂度都是O(log n)。

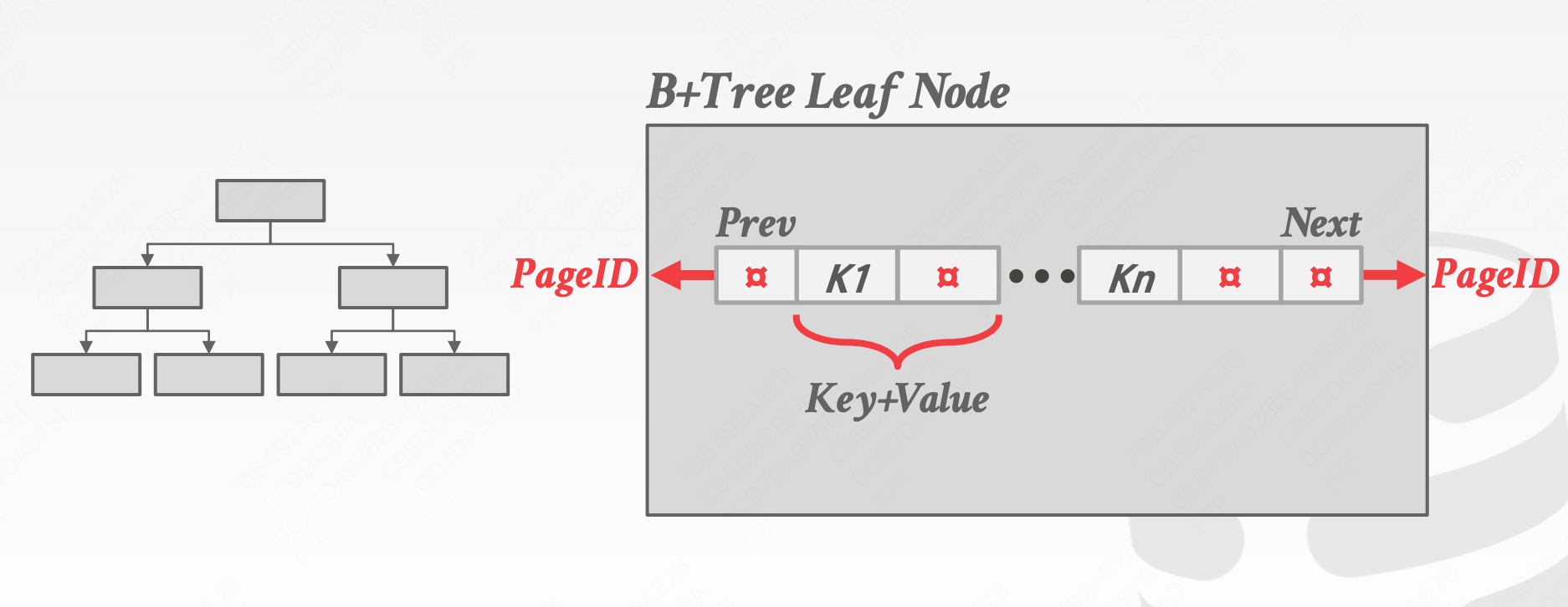
叶子节点的内容，通常key和value是分开存储的，因为搜索的时候并不需要加载value数据

元数据
- isleaf 是否是叶子节点
- slots 有多少空闲的slot
- prev 前一个叶子节点的指针
- next 后一个叶子节点的指针
key数据
value数据

结构：

B+树是一种多路自平衡的树结构，所有的叶子节点都在同一层，并且叶子节点通过链表连接。
它是MySQL中最常用的索引类型，支持范围查询、精确查找等操作。

优点：

高效的范围查询：由于B+树是顺序存储的，支持范围查询，查询某个区间的数据时非常高效。
高效的精确查询：B+树通过逐层查找，可以快速定位到数据行。
支持排序：由于叶子节点按顺序排列，B+树非常适合用于ORDER BY、GROUP BY等操作。
空间利用高：每个非叶子节点仅包含键，而不包含数据，可以节省存储空间。

缺点：

性能受页大小影响：B+树的性能与页的大小（每页存储的记录数）密切相关，过小的页会导致频繁的I/O操作，过大的页则会浪费内存。
写入性能较低：对于频繁插入、删除操作的场景，B+树索引的维护成本较高，可能导致性能下降。

应用场景：

最常用于主键索引、普通索引和唯一索引。尤其适用于需要进行范围查询、排序的场景。

特点：

b+ tree,保证每个节点都必须是半满的，对于存放在节点中的key数量来说，key数量至少为M/2 - 1个，M为树的高度，key的数量必须小于 M - 1,如果当删除数据以后导致key数量小于M/2 - 1个，就会进行平衡，使他满足M/2 - 1个。

M/2 - 1 ≤ key数量 ≤ M - 1
如果一个中间节点有k个key,那你就会有k+1个非空孩子节点，也就是k+1个指向下方节点的指针。每个节点的内容是一个指针和一个key
叶子节点之间有连接叶子节点的兄弟指针，这个想法来源于b link tree。每个节点的内容是一个数据和一个key，数据可以是一个record id 也可以是一个 tuple
b+ tree 标准填充容量大概是67% - 69%，对于一个大小是8kb的page来说，如果高度为4，大约能记录30 0000个键值对。
b+ tree的节点大小，机械硬盘的大小最好在1M,ssd的大小在10KB

示例图

B+树的叶子节点就是一个page，关于page的具体内容我们之前已经讲过了，不再赘述。我们将节点放大大概是这样的。

b tree 和 b+ tree 的区别

b tree的中间节点也可以存数据，所以key是不重复的
b+ tree的中间节点没有数据，所有数据都在叶子节点，所以key有可能既存在中间节点也存在叶子节点。会重复
b tree的性能在并行处理上更差，因为修改以后需要向上传播也需要向下传播修改，这个时候两边都要增加锁
b+ tree的性能更好，因为只修改叶子节点，所以只需要向上传播，只需要增加一个锁

b+ tree的查找

对于<a,b,c>,查找a=5 and b=3也是可以走索引的，但是hash索引就不行，有些数据库还支持b=3的搜索走索引，比如oracle和sql server

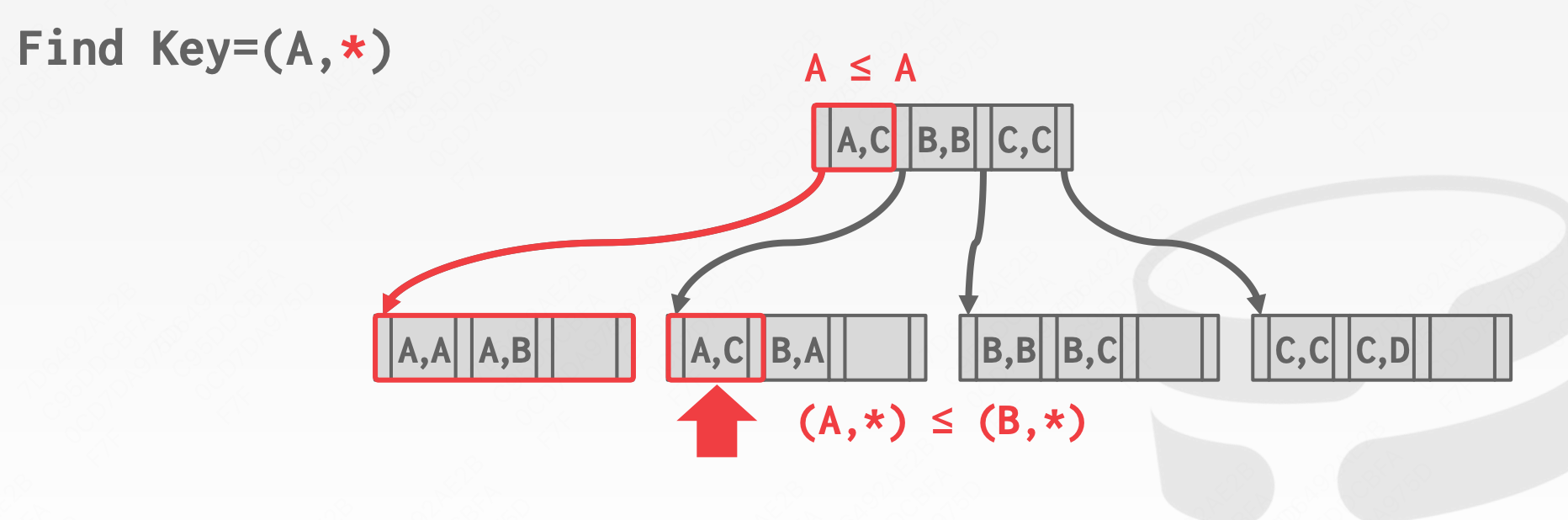
b+ tree还有一个方便的地方在于支持联合索引，我们可以设置A、B、C三个key的联合索引并支持查找。

假设我们查找A，B

假设我们查找A,*

假设我们查找*,A

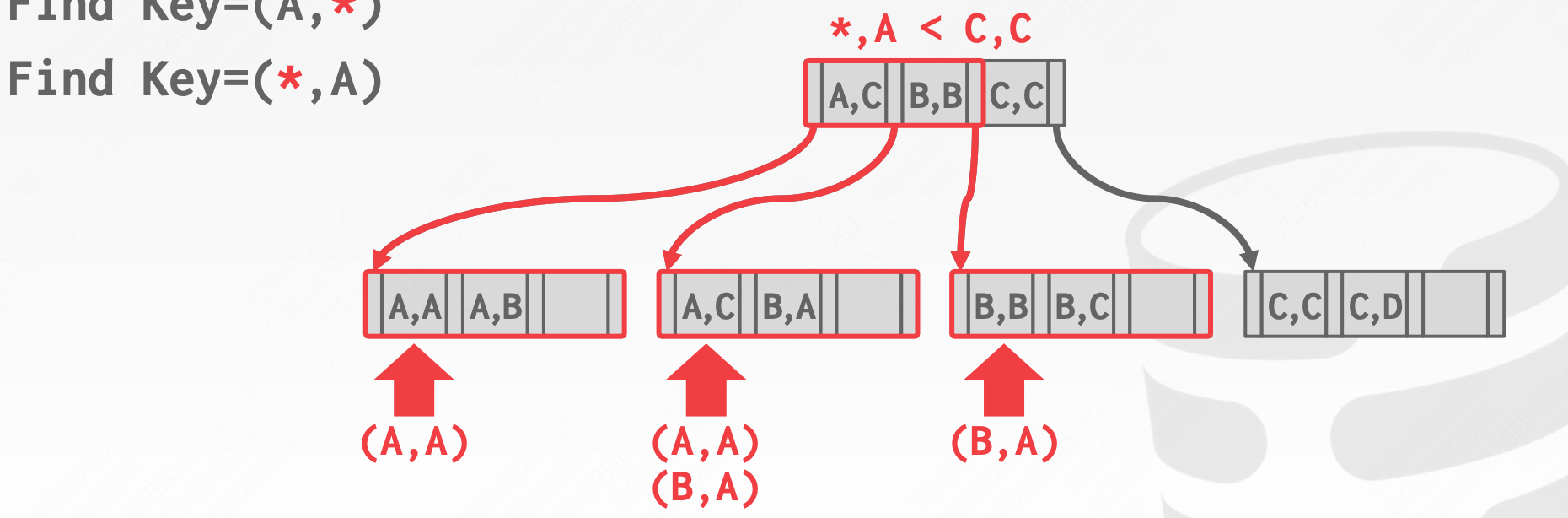
可以看到，对于b+树索引来说，这些查找都可以满足，这也是数据库支持联合索引的重点。

b+ tree 插入

向下扫描，找到对应的叶子节点
如果可以插入就直接插入
如果不可以插入，那么从中间分开，变成两个叶子节点，并将中间的key传递给父节点，插入父节点。
如果父节点可以插入就直接插入并分出一个指针指向新的叶子节点
如果父节点不可以插入重复上述操作3

我们来看一个实例：依次插入1,2,3,4,5,6,7，假设我们的度是3，也就是一个节点最多能容纳3个数据。

插入1

插入2，这个时候2个节点是在一起的

插入3，这个时候不可以插入了，因为插入就满了，因此要从中间分开，变成两个叶子节点。并将中间的key传递给父节点，插入父节点。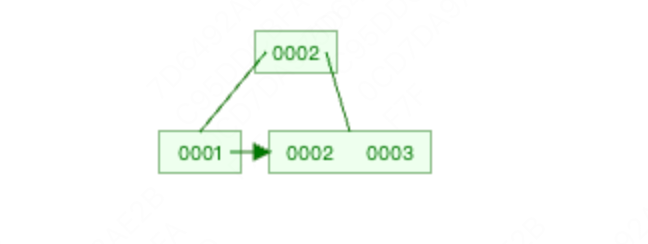

插入4，因为4插入到2，3节点中，导致再次分裂，分裂后，如下图所示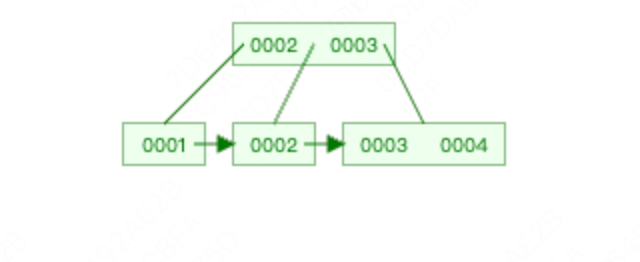

插入5，同样再次分裂，但是，父级也到达了3个数据，因此父节点同样分裂。最后结果如下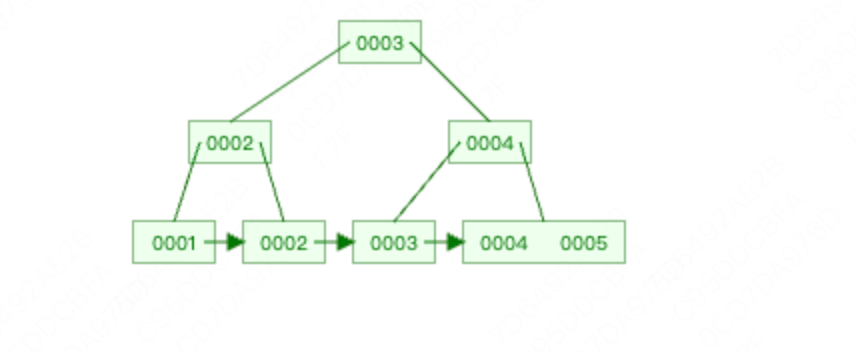

插入6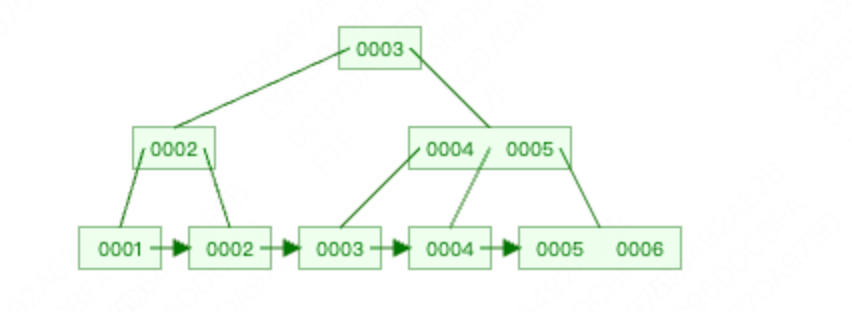

插入7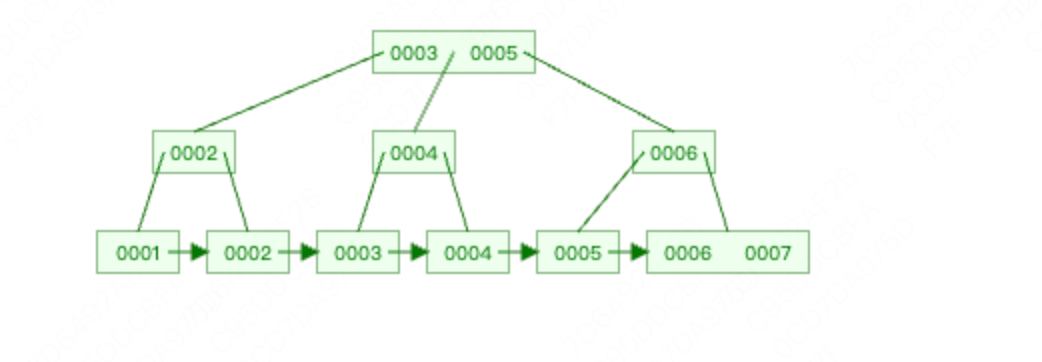

b+ tree 删除

向下扫描，找到对应的叶子节点，这个时候就会增加latch，因为不知道需不需要合并，操作以后才会释放
如果可以删除就直接删除
如果删除后导致key数量 < M/2 - 1,那么就会出发合并，因为不满足key数量啦
进行合并的时候删除这个key，然后先查看左右的兄弟节点，是否能直接把数据插入过来，如果可以的话就掠夺一个key过来，然后向上传播
如果不能掠夺，那么就合并到兄弟节点，然后向上传播。

我们接着上面的实例：依次删除1,2,3,4,5,6,7

删除1，因为删除后 key数量 < M/2 - 1，因此触发了合并逻辑。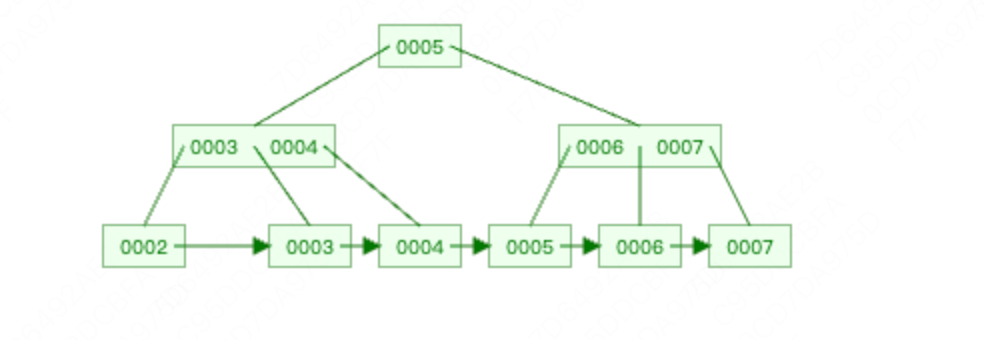

删除2，同样进行合并。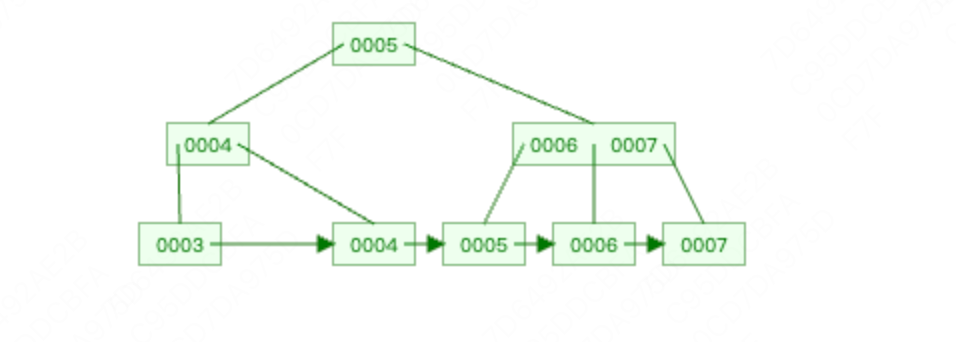

删除3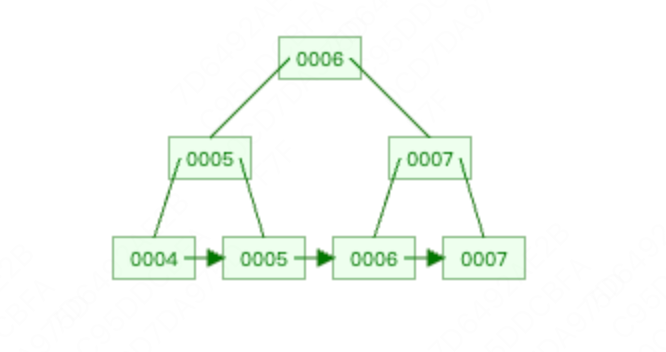

删除4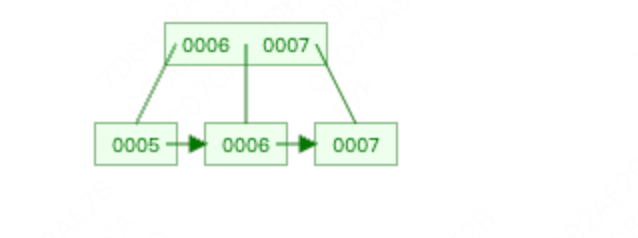

删除5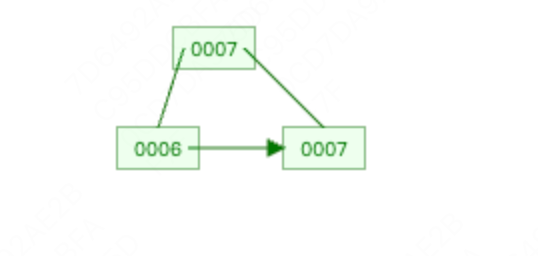

删除6

删除7以后，树就没了。

推荐书籍 Modern B-Tree Techniques

对于非唯一索引

重复存储，需要注意两个相同的key存储在不同的page中
value list,key只存储一个，然后所有的value存储成value list

节点内部的搜索

线性搜索
二分搜索
interpolation
- 通过数学计算出线性搜索的起点，提升搜索速度

优化方法

前缀压缩
- 比后缀截断用的更多
- 存储在page中的key,如果前缀一样的可以提取出来存储一次，然后剩余的数据在存储在key里面
后缀截断
- 存储在中间节点的，用来寻路的key，可以只存储前面的部分，如果后面的不需要可以截断
- 更新的时候需要进行维护
批量插入
- 如果已经有数据了再建立索引，这个时候不需要从头开始一个个建立，只需要先排序
- 然后建立所有的叶子节点
- 在一层层向上建立中间节点
- 非常普遍的方法，主流数据库都支持
point willizeing
- 将节点固定在内存中
- 对于page来说，直接存储page指针而不是page id，就不需要请求buffer pool了

b+ tree的重复key，通常使用增加record id的方式，这种方式影响更小。

增加record id,record id是page id + offset用来确定tuple的位置。
垂直扩展叶子节点，将数据存在里面

部分索引

在创建索引的时候添加where条件，只有符合条件的才会进入索引。
查询的时候只有符合条件的才会走索引

覆盖索引

在创建索引的时候添加联合索引
查询的时候所需数据都在索引中，就不需要在找对应的tuple信息了。

函数索引

创建索引的时候添加函数信息，比如 MONTH(date), 只对月份创建索引
查询的时候 MONTH(date) 就会走索引了，而date就不会走索引了
如果创建的时候只创建 date 索引，那么查询的时候 MONTH(date) 就不会走索引

trie index(前缀树)

把每个单词建立成树，一层放一个字母

radix tree

trie index的升级版
对于trie index进行了横向的压缩和纵向的压缩

结论

本文通过两个简单的实例，详细讲解了如何进行b+树的插入和删除操作，对于b+树了解以后，也知道是如何支持联合索引查询的了。

同时，还对比了其他几种数据结构。并提出了一些优化策略。

文末福利

关注我发送“MySQL知识图谱”领取完整的MySQL学习路线。
发送“电子书”即可领取价值上千的电子书资源。
发送“大厂内推”即可获取京东、美团等大厂内推信息，祝你获得高薪职位。
发送“AI”即可领取AI学习资料。
部分电子书如图所示。